          
Chapter 7 Reversibility and the Kelvin Temperature Scale
7-1 Reversibility and Irreversibility
Consider a process including 1) the system
proceeds from an initial state i to a state f;
2) the suspended object is lowered to
an extent that W unit of work are performed
3) a transfer of heat Q takes
place from the system to the series of reservoirs.
Local Surroundings: In the process above,
2) and 3) interacting directly with the system is called local surroundings.
Auxiliary Surroundings: (the rest of the
universe) In the process above, other mechanical devices and reservoir which are
accessible and which might interact with the system constitute the
auxiliary surroundings.
In the above process, at the conclusion of the
process, ( that is system is at final state f), the system maybe restored
to its initial state i, the object lifted to its former level and the
reservoir caused to part with the same amount of heat Q, without
producing any changes in the rest of the universe. Therefore, the above process
is said to be reversible.
Reversible process : a
reversible process is one that is performed in such a way that, at the
conclusion of the process, both the system and the local surroundings may be
restored to their initial states, without producing any changes in the rest of
the universe.
All nature process is irreversible.
7-2 External Mechanical Irreversibility
The processes involving the isothermal
transformation of work through a system (the state of system remains unchanged)
into internal energy of a reservoir.

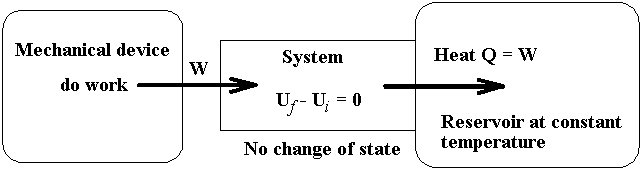
The examples for the process described in the
above diagram are
1) Irregular stirring of a viscous liquid in
contact with a reservoir.
2) Coming to rest of a rotating or vibrating liquid
in contact with a reservoir.
3) Inelastic deformation of a solid in contact
with a reservoir.
4) Transfer of electricity through a resistor in
contact with a reservoir.
5) Magnetic hysteresis of a material in contact
with a reservoir.
The reversed processes of the processes describe
above is not allowed by the second law, because to restore the system and
its local surroundings to their initial states without producing changes
elsewhere, that is an amount of heat, Q, would have to be extracted from the
reservoir and converted completely into work, is not allowed according to the
second law.


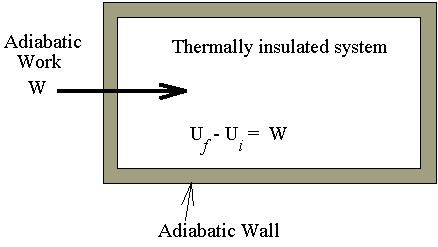
The examples for the process described in the
above diagram are
1) Irregular stirring of a viscous thermally
insulated liquid.
2) Coming to rest of a rotating or vibrating
thermally insulated liquid.
3) Inelastic deformation of a thermally
insulated solid.
4) Transfer of electricity through a thermally
insulated resistor.
5) Magnetic hysteresis of a thermally insulated
material.
The temperature of those systems going through
this type of process are changed, temperature rise from qi
to qf.
The reversed processes are also not allowed by the second law, because, to low
the temperature from qf
to qi,
meanwhile an amount of heat Uf - Ui
will be extracted and converted completely into work, this is not allowed by the
second law.

The two different type of processes described
above, are related to the transformation of work into internal energy of either
a system or of a reservoir, and all the processes related to the effects of
viscosity, friction, inelasticity, electric resistance and magnetic hysteresis.
These effects are known as dissipative effects. and the work is
said to be dissipated.
External Mechanical irreversibility :
Processes involving the dissipative work into internal energy are said to
exhibit external mechanical irreversibility.
Perpetual Motion Machine of the First Kind
: The machine did not obey the first law, i.e. it can create energy.
Perpetual Motion Machine of the Second Kind
: The machine did not obey the second law, i.e. it can convert all the work into
heat.
Perpetual Motion Machine of the Third Kind
: The machine can eliminate all the dissipative effects.
7-3 Internal Mechanical Irreversibility
The following processes are very important
natural processes, they are internal mechanical irreversibility, for example
1) Ideal gas rushing into a vacuum (free
expansion).
2) Gas seeping through a porous plug (
throttling process).
3) Snapping of a streched wire after it is
cut.
4) Collapse of a soap film after it is
pricked.
These processes involve the transformation of
internal energy of a system into mechanical energy and then back into internal
energy again. All these processes are irreversible. Let us prove the free
expansion is irreversible. For free expansion process, the followings are true
a) No interaction →
no local surroundings.
b) Temperature are the same before and after
the free expansion.
c) The volume of the ideal gas system is
expanded from Vi to a larger volume Vf.
To restore the system to its initial state,
a) Gas would have to be compressed
isothermally to the volume Vi.
b) Assume the isothermal compression is
quasi-static process, also no friction.
c) An outside mechanical device has to do
work W to compress the ideal gas and has its volume return to Vi.
d) The work done by the outside device will go
through the system and become heat. The heat then flow into the reservoir
( keep the system unchanged ) which has the same temperature of the
system.
e) The local surroundings should not change for
reversible process, thus the heat should be extracted from the reservoir and
converted into work to have the mechanical device return to its initial state.
To have all the heat became work is impossible,
as we know from the second law. So the last step e) can not be accomplished. So
free expansion process is an irreversible process.

Free expansion is
1) Internal energy →
Kinetic energy : Gas molecules move
through valve to vacuum, thus Mass motion or Streaming of gas molecules is the
sign of the gain of kinetic energy.
2) Kinetic energy → Internal
energy : This kinetic energy is
dissipated through viscosity into internal energy again.

Cut the stretched wire is
1) Internal energy →
Kinetic energy : Kinetic energy of
irregular motion and of vibration after it have been cut.
2) Kinetic energy → Internal
energy : This kinetic energy is
dissipated through inelasticity into internal energy again.

From the examples of free expansion and cut the
stretched wire processes, first energy is transferred into kinetic energy as
result of mechanical instability and second due to the dissipative effect the
kinetic energy converted into internal energy. →internal
mechanical irreversibility.
7-4 External and Internal Thermal Irreversibility
External thermal irreversibility :
Transfer heat between a system and reservoir by virture of a finite temperature
difference:
1) Conduction or radiation of heat from a
system to a cooler reservoir.
2) Conduction or radiation of heat through a
system (which remains unchanged) from a hot reservoir to a cooler one.
The reversed process ( if they are reversible)
has to have heat transferred from the cooler reservoir to the hot reservoir
without doing any work to change the state of system and the rest of universe,
this violate the Clausius statement of the second law.
Internal thermal irreversibility : Heat
is transferred between part of the same system because of non-uniformity of
temperature.
7-5 Chemical Irreversibility
A spontaneous change of internal structure,
chemical composition, density, crystal form etc.
7-6 Conditions for Reversibility
The processes discussed above, also living
processes (such as cell division), are irreversible. It is a direct consequence
of the second law of thermodynamics that all natural spontaneous processes
are irreversible.
Most of the natural processes have the following
two properties
1) can not satisfy thermodynamic equilibrium
conditions, neither mechanical, thermal or chemical equilibrium.
2) involve dissipative effect, such as
viscosity, friction, inelasticity, electric resistance and magnetic hysteresis.
A process will be reversible then 1) it is
performed quasi-statically and 2) it is not accompanied by any
dissipative effects. Since it is impossible to satisfy these two conditions
( in laboratory can approximately reach these two condition in some degree),
thus a reversible processes are purely an ideal abstraction, the purpose of
their existance is for theoretical calculation.
For a heat reservoir, the processes of the
heat enters and leaves the reservoir are reversible, the changes that take place
(when heat enters and leaves) in the reservoir are the same as those which would
take place if the same quantity of heat were transferred reversibly.
7-7 Existence of Reversible Adiabatic Surfaces
From the second law of thermodynamics, we have
been told that all netural, spontaneous processes are irreversible. There are
two ways to develop further consequences based on the second law; they are:

Engineering Method :
1) Due to Carnot, Kelvin, and Clausius;
2) This method is based on the Kelvin-Plank
statement or Clausius statement of the second law to formulate.
3) Starts with Carnot cycle which is a reversible cycle including two
adiabatic processes and two isothermal processes.
4) The ideal engine which is based on
Carnot cycle has the highest efficiency operated between two different
temperature reservoirs, compared with any other engine operated between the
same two different temperature reservoirs.
5) Any ideal engine (regardless of the system of
the operated engine) operated at between the same two different temperature
reservoirs have the same efficiencies.
6) The Kelvin temperature is defined (based on
the Carnot cycle) so as to independent of any particular kind of thermometry.
7) The Clausius theorem is derived and entropy
function is introduced.

Axiomatic Method : Based on the physical
concepts and expressed it in mathematical language.
1) Due to Caratheodory, all the consequences
of the Caratheodory axiom follow directly from the Kelvin-Plank statement of
the second law.
2) Study the behavior of systems, their
equation of states and their coordinates, their physical properties and their
processes.
Axiom expressed by Caratheodory : In the
neighborhood (however closed) of any equilibrium state of a system of any number
of thermodynamic coordinates, there exist states that cannot be reached ( are
inaccessible) by reversible adiabatic processes.

We can derive the Kelvin temperature scale from
this axiom, and all the consequence of the engineering method. First define the
thermodynamic coordinates, they are temperature t, a generalized
displacement X and generalized force Y. The first law can be
expressed as
If the equation of state are known, then only
two of the thermodynamic coordinates are independent. If U is
function of t and X, then
thus
where 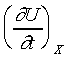 , ,
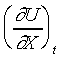 and Y are known functions
of t and X. For the reversible adiabatic process of the system,
the equation can be written as and Y are known functions
of t and X. For the reversible adiabatic process of the system,
the equation can be written as
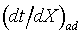 represents the slope of an adiabatic process on a tX diagram at all
points. Therefore the above equation has a solution of a family of adiabatic
curves, this solution is defined as
represents the slope of an adiabatic process on a tX diagram at all
points. Therefore the above equation has a solution of a family of adiabatic
curves, this solution is defined as


For example: the ideal gas; PVg
= Const. or TVg-1
= Const.
For ideal gas, we have the forllowing relations;

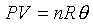

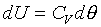

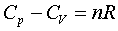

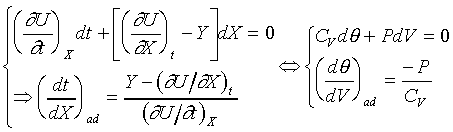

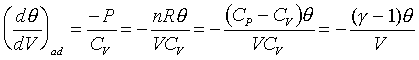

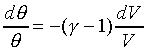 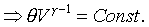


Different constant value in the above equation
represents different adiabatic curve. The existence of the family of curves 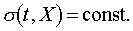 ,
representing reversible adiabatic processes, follows from the face that there
are only two independent coordinates used to describe a system
obeying the first law of thermodynamics. ,
representing reversible adiabatic processes, follows from the face that there
are only two independent coordinates used to describe a system
obeying the first law of thermodynamics.
When three or more independent coordinates
are needed to describe a system, the second law is needed to
assure the existence of the adiabatic curves.
Through any arbitrary initial-state point,
all reversible adiabatic processes lie on a surface, and reversible adiabatics
through other initial states determine a family of nonintersecting surfaces.
Consider a system has five thermodynamic
coordinates, thus 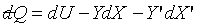 . There are two
equations of state, so only three coordinates are independent, let us choose
them as U, X, X'. . There are two
equations of state, so only three coordinates are independent, let us choose
them as U, X, X'.
There are two reasons to choose three
independent coordinates
1) Can draw three dimensional graphs by using
these three coordinates.
2) The conclusion gets from three independent
coordinates is a general result, can generalize to the system with any number
of independent coordinates.
First let us prove that states have the same
value of X and X' can not be reached by reversible adiabatic processes from the
same initial state, that is, the states whose X and X' are the same are in the
different adiabatic surfaces. In the following diagram, f1
and f2 are two equilibrium states, and both states
have the same value of X and X'. We can prove that both states f1
and f2 cannot be reached by reversible
adiabatic processes from i. (利用反證法)
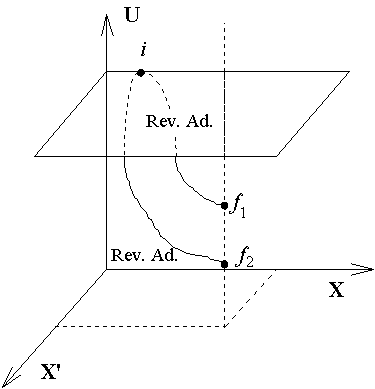
A) Assume i →
f1 and i →
f2 are reversible adiabatic processes, thus no
heat is transferred but work W is done.
B)The work done by the process from f1
→ f2 is
zero, since X and X' are kept constant in this process.
Therefore heat Q has to be absorbed to increase the internal energy
from f1 → f2.
C) Then in the cycle, i →
f1 → f2
→i, there is no energy change,
thus W = Q, and this result violates the Kelvin-Plank statement
of the second law of thermodynamics. So that both f1
and f2 can not be reached by reversible
adiabatic processes.
We can conclude that 『Only
one point on the line of constant X and X" can be reached by a reversible
adiabatic process from i』.
For every line parallel to U-axis, there exists
only one point which is accessible by the reversible adiabatic process from
initial state i. So 『The locus
of all points accessible from i by reversible adiabatic processes is a
space of dimensionality one less than three, in other words, these points
lie on a two-dimensional surface.』
To generalize the above discussion to the system
having more independent coordinates, we can consider a system have four
coordinates. If a system is described by four independent coordinates, for a
given equilibrium state i, then the states accessed by i through a reversible
adiabatic processes would lie on a three-dimensional hypersurface, and so on.
The three independent coordinates in the above
discussion are U, X and X', and there is a reversible
adiabatic surface for a give state i, which is function of U, X
and X'. We can also change the independent coordinates to t, X
and X', and it is equivalent to the U, X and X',
then the shape of reversible adiabatic surface for a given state i may be
different, but it is still a surface. U = U(t,X,X')
and two equations of state thus U, X and X' can be
treated as independent varibales, also the t, X, and X'.
Since t, X and X' are
independent varibales, so U can be expressed as function t, X
and X', or U can be treated as independent variable as we did
above. Hence for a given equilibrium state i, the reversible adiabatic
surface can be written as function of t, X, and X'. that is
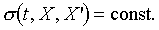 . .
For the above discussion we know that :
Reversible adiabatic surfaces cannot intersect.
7-8 Integrability of 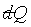
對於一個系統只有兩個獨立變數,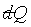 的積分是容易達成的。例如:理想氣體的等溫過程,因為 的積分是容易達成的。例如:理想氣體的等溫過程,因為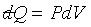 且
PV = nRq,故 且
PV = nRq,故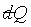 可積分。 可積分。
對於一個系統有兩個以上的獨立變數時,由於熱力學第二定律,及溫度是不同狀態方程式中共用的變數,所以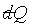 也是可積分的。 也是可積分的。
If a system can be described by three independent coordinates, t, X,
and X', then
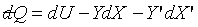 and and 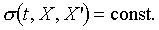 . .
thus we may take U as function of s,
X, X'. (treat them as independent variables) So;
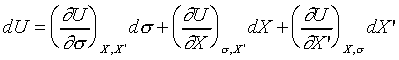
and
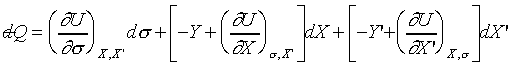
(Since s , X and X' are
independent variables.)
a) If two differentials ds and dX
are zero, then dX' has to be zero too. Since ds
= 0, we have s = constant, the it is a
reversible adiabatic process → 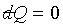 . .
b) By the same token, if ds and dX'
are zero, then dX has to be zero.
In order for the coordinates s, X, X'
to be independent, and also for 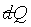 to be zero whenever ds is zero, then
to be zero whenever ds is zero, then
Define :
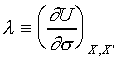 → → 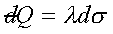 . .
and 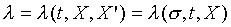 , the above equation can
multiplied by 1/l, the result is an exact
differential ds. It is only because of the
existence of the second law that the differential form referring to a
physical system of any number of independent coordinates possesses an
integrating factor. , the above equation can
multiplied by 1/l, the result is an exact
differential ds. It is only because of the
existence of the second law that the differential form referring to a
physical system of any number of independent coordinates possesses an
integrating factor.
For a reversible adiabatic surface, it follows 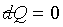 ,
but the equation between two infinitesimally neighboring reversible adiabatic
surfaces is ,
but the equation between two infinitesimally neighboring reversible adiabatic
surfaces is 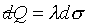 . See figure 7-6. . See figure 7-6.
When a reversible process is represented by a curve connecting the two
surfaces, however, heat 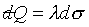 is
transferred. is
transferred.
All curves joining the two surfaces represent processes
1) with the same ds, (因為每一個絕熱面的s為一常數,故面與面間的差亦為一常數)
2) but the value of l are different. (l
與路徑相關,因為dQ與路徑相關,且l是t、s、X的函數)
7-9 The Physical Significance of l
l是t、s、X的函數,首先讓我們找l與溫度的關係。考慮兩個系統與同一熱庫相連(即兩者有相同溫度),且各有三個獨立變數。
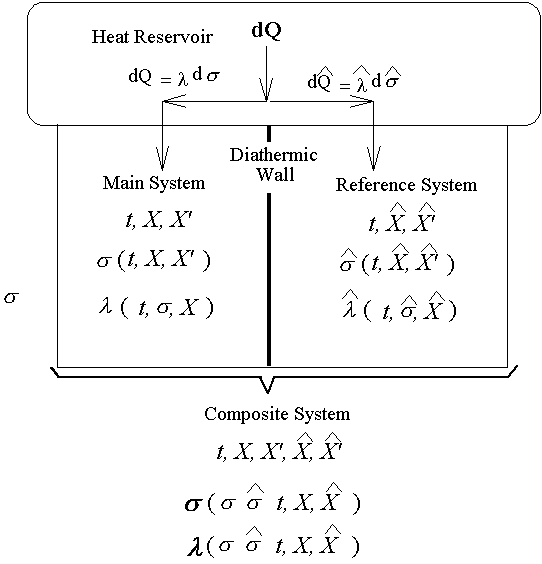
The main system and reference system are assumed to be at all times in
thermal equilibrium.
在組合系統中在兩個Reversible
adiabatic hypersurfaces 間的過程仍可以有如下的關係:
比較兩個ds的式子,得
也就是說s與t、X和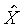 無關,而僅與s和 無關,而僅與s和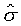 相關。 相關。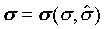 ,比較系數後得 ,比較系數後得
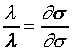 且 且
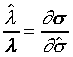
上式中所顯示的比值也與t、X和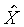 無關。 無關。
注意:是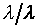 、 、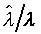 比值與t、X和 比值與t、X和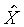 無關,而其各自本身仍是溫度的函數。若l僅是s的函數,即 無關,而其各自本身仍是溫度的函數。若l僅是s的函數,即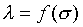 ,則 ,則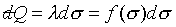 變成是一全微分式,而是非正合微分,故l不僅僅是s的函數,還必需是溫度的函數,即 變成是一全微分式,而是非正合微分,故l不僅僅是s的函數,還必需是溫度的函數,即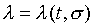 。 。
所以
由上的討論、即對於任何數目獨立變數的系統,一定有
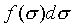 是正合微分,f(t)是一經驗溫度t的任意函數。而1/f(t)是 是正合微分,f(t)是一經驗溫度t的任意函數。而1/f(t)是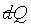 積分因子。 積分因子。
一) 此積分因子僅是溫度的函數。
二)
對於所有的主系統、參考系統和組合系統等任何系統,積分因子都相同。
也就是因為如此,依據積分因子的特性,使得我們可以定義出絕對溫度。
(The integrating factor is a function of temperature only
and that it is the same function for all systems.)
7-10 Kelvin Temperature Scale
考慮一系統有三個獨立變數,t、X和X',兩個等溫面和可逆絕熱面如圖7-8所示。如果系統經由一可逆等溫過程從溫度t的等溫面與可逆絕熱面sI相交的狀態b、變化到溫度t的等溫面與可逆絕熱面sII相交的狀態c時,此過程中熱量Q可以被計算
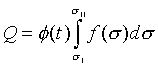 ( at constanat t ) ( at constanat t )
若可逆等溫過程從溫度t3的等溫面與可逆絕熱面sI相交的狀態a、變化到溫度t3的等溫面與可逆絕熱面sII相交的狀態d時,此過程中熱量Q3可以被計算
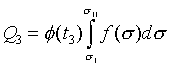 ( at constanat t3
) ( at constanat t3
)
上兩式的比值為
而凱氏溫標是由下式定義的,
上式說明凱式溫度的定義是與在等溫面上一等溫過程由一可逆絕熱面轉換至令一個可逆絕熱面所吸收之熱量有關。由此定義的凱式溫標與物質的特性無關。
『Two temperature on the Kelvin scale
are to each other as the heats trasnferred between the same two reversible
adiabatic surfaces at these two temperatures.』
若將T3定為水三相點的溫度,273.16
K,則凱氏溫標的定義是
其中熱量的測量均是對相同的兩個可逆絕熱面之間。
而絕對零度的定義是:
If a system undergoes a reversible isothermal process between two
reversible adiabatic surfaces without transfer of heat, the temperature
at which this process takes place is called absolute zero.
一) 絕對零度與物質的特性無關,
二)
實驗上是否可以達到絕對零度?
7-11 Equality of Ideal-Gas Temperature and Kelvin Temperature
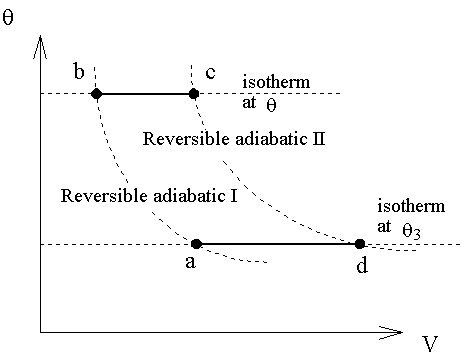
一理想氣體經一微小可逆過程,由第一定律可以得下式,
由b→c的等溫過程中,熱量的變化為
而a→d的等溫過程中,熱量的變化為
所以兩式相除後得:
由a→b是絕熱過程,則
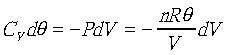 , ,
積分以後得
由d→c也是絕熱過程,則
從上兩式得知
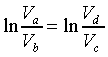 且 且 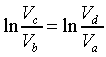
即
若選取相同的參考溫度,例如水的三相點溫度,即qTP
= TTP = 273.16 K,則理想氣體溫度與凱式溫度的數值是完全相等的→q
= T。
| 