Chap 1: 熱力學：熱物理學：(Thermodynamics)
何謂熱力、熱物理學→我以為是最人性化的一支物理與自然界最有密切關連。
Classical Physics have three branches： Mechanics－Dynamics
of particles acted upon by forces
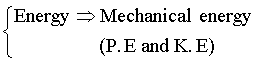
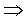Newton's
law.(Lagrange. Hamilton Principle) E.M. Theory－Dynamics
of fields that mediate those forces
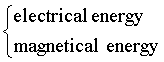
Maxwell
equations. Thermodynamics－Apply to all
Types of systems in macroscopic aggregation.
It does not predict specific numerical values
for observable quantities, but It sets limits (inequalities) on permissible
physical processes, also establishes relationships between (among) apparently
unrelated properties.
Thermodynamics：
與其他物理最大的不同在於其可以應用至任何系統，it
is not based on a new and particular law of nature, 
it
only reflects a commonalty or universal feature of all "Laws".
Thermodynamic System
Macroscopic
System: Thermodynamics describes only (static states, equilibrium) of
macroscopic system.
問：人可以看到的最小空間是多小??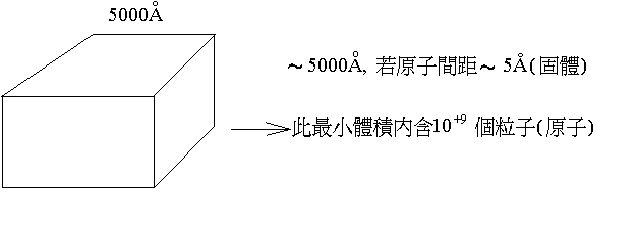 
在力學中每一個粒需要三個空間作標來描述，但109個粒子，其運動狀態能否用力學的座標來描述呢??答案是相當困難，即使是最近流行的用電腦模擬(以牛頓運動定律為基礎的Molecular
Simulations)至多也祗可以模擬幾百個粒子的運動。這個的系統就是一個巨觀的系統，就必須用熱力學的座標來描述。
問：What is the smallest time interval can be
detected by man ?? ∼10-2sec
或10-1sec之間。而原子振動的周期∼10-15sec，所以可以測得的值基本上是一種時間上的平均值，例如壓力，......。
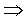Macroscopic
coordinates are time-independent, they are time average and spatial average.
根據上述討論我們可以給出一個所謂的熱力學系統的完整定義:
Thermodynamic system :
Macroscopically homogeneous, isotropic and uncharged, that are large enough so
that surface effects can be neglected, and that are not acted on by electric,
magnetic and gravitational fields. 且此系統仍然遵守基本物理定律：能量守恆定律。熱力學系統中所討論的熱力能量(如化學位能、內能、自由能等)，多半只有他們的差值才具有物理義意(如第一定律)，或是關係式，如熱力學的Maxwell
equations 就是一個很好的例證。 Macroscopic
Coordinates is
1: They involve no special assumptions
concerning the structure of matter.
2: They are few in number.
3: They are suggested more or less directly by
our sense perceptions.
4: They can generally be directly measured.
問: 什麼是熱平衡(Thermal
equilibrium)
熱力學第零定律：
a與b分別與c達成熱平衡，則a和b也達成熱平衡
溫度的定義：若A和B成熱平衡，(thermal
equilibrium)，則A和B有相同的溫度。比較Logic的說法是：
系統的溫度是一種性質，這性質決定此系統是否與其他的系統達成熱平衡(thermal
equilibrium)。
問:什麼是isothermal?
對於溫度比較嚴格的證明：
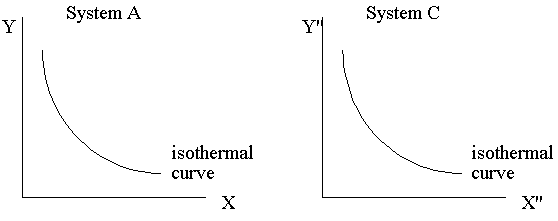
When System A and C approach thermal
equilibrium, then the final state of thermal equilibrium is denoted by a
relation among these coordinates, and may be written in the general functional
form:
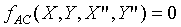(例如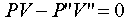
)
Similar argument can be applied to B and C, when
B and C approach thermal equilibrium,
When B and C approach thermal equilibrium, we
have
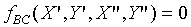
Assume: Both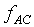 
and 
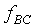are well behaved function, so
we can solve for X"
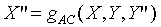
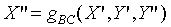
i.e.: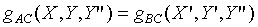 
根據第零定律，系統A和系統B也是處於熱平衡的狀態，故
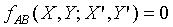
但是
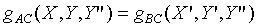
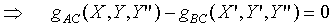
根據第零定律；上式必需與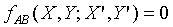
具有相同的形式，所以上式中的Y"可以被刪除，因為
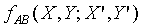並不是Y"的函數。故
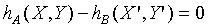與Y"無關，而得
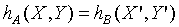
同理可以證明:
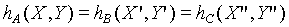
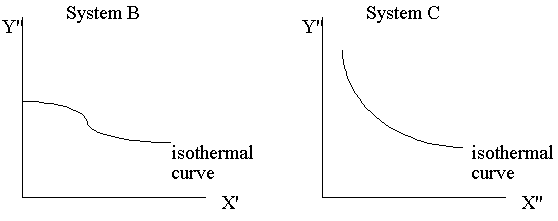
上式說明當A，B和C達成熱平衡時，存在一個個別系統熱力學坐標的函數，且這個函數值(即使系統熱力學坐標都不相同)對於達成熱平衡的系統都相同，於是我們給予這個函數一個名稱----經驗溫度t。(日後會證明經驗溫度與絕對溫度是相等的)
即
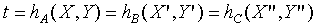
而此處的h函數，代表上述圖中的等溫曲線組。溫度的量測→如何制定溫標
定義t的刻度的方法→即是溫度計制定的基準，
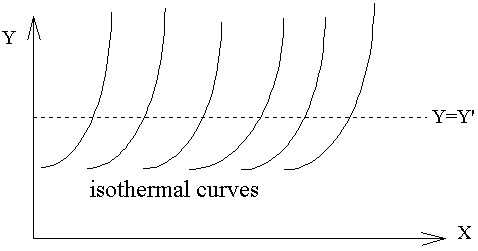
先在熱力學坐標XY平面上找出等溫曲線組，再視方便選定X或Y為定值，如上圖中選定Y=Y'的定值，則X的值隨溫度的變化而改變，因而當我們選定一參考點溫度的數值，則可以由X值隨溫度變化標示出溫度的刻度，故溫度計的方程式為
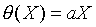
其中a是由選定的參考點溫度而定。一般認定水的三相點為標準溫度固定點，因為水的三相點溫度為273.16K，所以
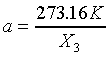
其中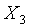
是水三相點時X的值。所以當Y為常數時(Y=Const.)，溫度計的方程式為
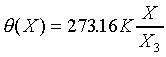
由上的討論知；只要找出一個熱力學坐標隨溫度變化的函數(其餘的熱力學坐標保持不變的條件下)，選定水的三相點為參考點，則可以制定溫度計了。以下介紹三種溫度計；
一) 定容氣體溫度計：即Y=體積V=常數，而X=壓力P，P隨溫度的變化則可以表示
溫度。
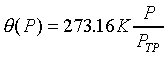
問：不同的氣體裝入定容氣體溫度計，在測量相同溫度時，是否讀數相同？原因是為何？
問：何為理想氣體溫標？ 答：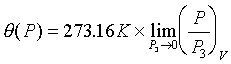
二) 電阻溫度計：R表電阻
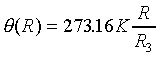
三) 熱電偶溫度計：e表電位差
