|
          
Chapter 5�G�z�Q����
5-1 ���骬�A��{���G
�z�Q����żУc�F�w�q�O�]�w�e�ūp�^ 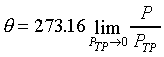 �A�]��P�M �A�]��P�M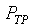 �ͪ��s�ɡ^
�c�P���骺����L���C���O��P�M �ͪ��s�ɡ^
�c�P���骺����L���C���O��P�M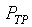 ���ͩ�s�ɡA�U�خ������ܪ��ȳ����P�A���ܻP���饻�観���]��1-8�^�p�G�O���b�w�Ū�����F���q�䤣�P������nv�ά۹��������OP�èD�䭼�nPv�A�hPv�i�H��Virial
Expansion����k�i�}�]������H�H�H�^�]Pv�i�H�����K�ת���ơA����q�O���@�w�ɡA�h�i�H����1/v����ơA�o�N�O������n��Virial
Expansion�C�^�F�Y ���ͩ�s�ɡA�U�خ������ܪ��ȳ����P�A���ܻP���饻�観���]��1-8�^�p�G�O���b�w�Ū�����F���q�䤣�P������nv�ά۹��������OP�èD�䭼�nPv�A�hPv�i�H��Virial
Expansion����k�i�}�]������H�H�H�^�]Pv�i�H�����K�ת���ơA����q�O���@�w�ɡA�h�i�H����1/v����ơA�o�N�O������n��Virial
Expansion�C�^�F�Y 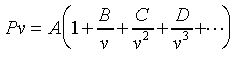 A�BB�BC���٤��������Y�ơA�ҦpA���Ĥ@�����Y�ơAB���ĤG�����Y�Ƶ��C�P������l���S�ʦ����C�b0��40atm�����O�d���APv�M1/v��ڤW�O���u�ʪ����Y�C�b�����p���W�A�����Y�G�Ӻ����Y�ơAA�MB�����j�N�q�C�����O�U���һݦҼ{�������Y�ƴN�U�h�C------������C��5-1����ܩT�w�ūɡA��P���s�U�خ��餧Pv���n�ͪ�@�өw�ȡF�Y A�BB�BC���٤��������Y�ơA�ҦpA���Ĥ@�����Y�ơAB���ĤG�����Y�Ƶ��C�P������l���S�ʦ����C�b0��40atm�����O�d���APv�M1/v��ڤW�O���u�ʪ����Y�C�b�����p���W�A�����Y�G�Ӻ����Y�ơAA�MB�����j�N�q�C�����O�U���һݦҼ{�������Y�ƴN�U�h�C------������C��5-1����ܩT�w�ūɡA��P���s�U�خ��餧Pv���n�ͪ�@�өw�ȡF�Y
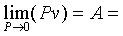 �ūפ���ƻP����L�� �ūפ���ƻP����L��
�z�Q����ūשw�q�O�G 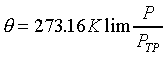 �]��n�P���ռƫO���@�w�^ �]��n�P���ռƫO���@�w�^
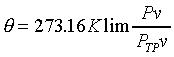 -----��------- -----��-------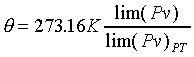
�Y
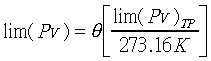
�ҥH�z�Q����`�ƧY
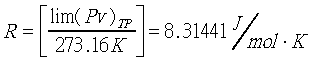
�ҥH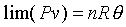
�w�q�G
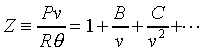
�i�H�Χ@�Ϫk�D�oB�MC�F����5-2��v�]Z-1�^V.S.1/v�@�ϡA�h�PY�b�����I�Y��B�A�ӱײv��C�G
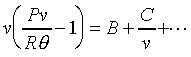
PS. ��5-2�����G�P��5-1�۲ŦX�C
5-2 ���骺����
�ھڲĤ@�B�ʩw�ߡA�b�ۥѿ��Ȫ��L�{���AQ�MW���O�s�A�ҥH�t�Ϊ�����O������----���O�t�Ϊ��ūO�_���ܤƩO�H�H�Y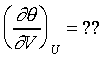 ���t�ƺ٤���Joule
Coefficient�F�o�˪������٤���Joule
effect�C �@��Ө��GU=U(V,�c)��U=U(P,�c) ���t�ƺ٤���Joule
Coefficient�F�o�˪������٤���Joule
effect�C �@��Ө��GU=U(V,�c)��U=U(P,�c)
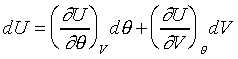
�b�ۥѿ��ȹL�{�����FdU=0�F�Yd�c=0�]�Y�S���ūת��ܤơ^�h
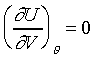 �F���y�ܻ��Y����P��n�L���C�Y��U=U(P,�c)�Ӫ��ܫh�G �F���y�ܻ��Y����P��n�L���C�Y��U=U(P,�c)�Ӫ��ܫh�G
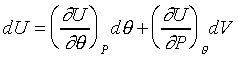
�Y�b�ūפ��ܪ����ΤU�A�g�Ѧۥѿ��Ȫ��L�{�FdU=0�Bd�c=0�F�h
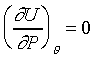
�]�N�O������P���O�L���C�ѤW�z���Q�ץi�H���D�F���i��ۥѵȮɡA�Y�ūרS���o���ܤơA�h���ण�O��n�M���O����ƦӶȻP�ū����YU=U(�c)�C���F�n��s�ۥѿ��P�ūת����YJoule�]�p�p�U������G
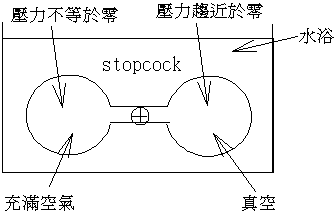
�N�}�����}�H��A����ۥѿ��Ȩ�u�ų����A���q���ȫe�᪺���šA�h�i�H���DFree
expansion�P�ūת����Y�C���O���P�e�������e�q�O���骺�@�d�����k�A�ҥHJoule�L�k���X����ūת��ܤơA���ƹ�W���骺�ū|�U�����C�Ө��O���ѤF�C������H�H�H���]��Cwater,C�e��>>Cair
�{�N��s���餺�����(�p�U�ϩҥ�)�O���q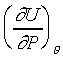 ���ȡF�O�Q�Τ@�ӬJ���@�\�S�����Ǿɪ����ſ��ȹL�{�C��5-3 ���ȡF�O�Q�Τ@�ӬJ���@�\�S�����Ǿɪ����ſ��ȹL�{�C��5-3
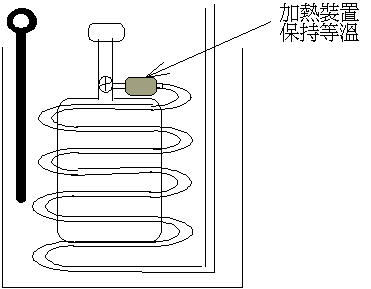
�o�{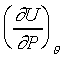 ���O�ūת���ƻP���O�L�� ���O�ūת���ƻP���O�L��
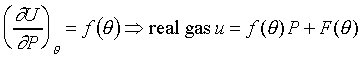
5-3 �z�Q����
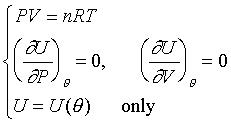
�b0-2atm���d���F�u�ꪺ����i�H�Q�����z�Q����~�t�X%�Ӥw�C���R�y��t�ΡGPV=nRT�G
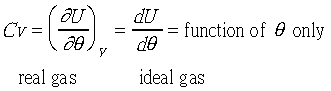
�b�w�������ΤUdP=0��dP/d�c=0
�B
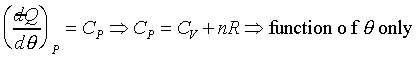
�B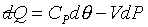
5-4 ���e�q��������q
���骺���e�q�O�Q�ιq�m��k�Ӵ��q�ACv�����q�O�N����m��@�D�`�����K�e������n�O���@�w�A�~¶�[
�����q�����G
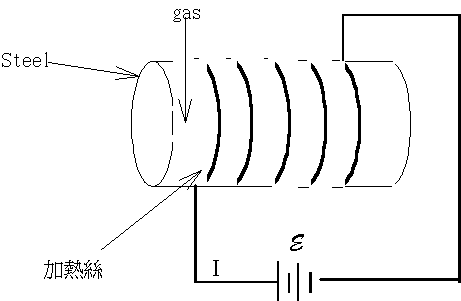
�Q�ΤU���� �h�i�H�DCV 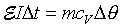 �Gt���ιq�[���ɶ��A�G�c���b���ɶ����ūת��ܤ�,m�����骺��q�A�hcv
���۹������w�e����A
�Gt���ιq�[���ɶ��A�G�c���b���ɶ����ūת��ܤ�,m�����骺��q�A�hcv
���۹������w�e����A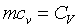 CP�����q��k�PCV�����F������O�������O�ҥH�ή���O�������O�y�L�@���q�p�A��������q�L�ᤧ�Ůt�A���骺�y�q�h�i�H�p��w�����e�q�F�]��
CP�����q��k�PCV�����F������O�������O�ҥH�ή���O�������O�y�L�@���q�p�A��������q�L�ᤧ�Ůt�A���骺�y�q�h�i�H�p��w�����e�q�F�]��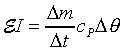 �b�C�������p�U�A���窺���G�P�z�Q����۪��A(�w�qcV�McP�����ռ��e�q)�z�Q���馳�U�ҩʽ�G(���ҥ���110��)
1�GcV is a function
of �c only 2�GcP
is a function of �c only 3�GcP��cV
= const. = R 4�G�^=cP/cV
= a function of �c only and >1 �C���ɪ����l����G�pHe,Ne�MAr�Τj�h�ƪ��ݻ]��pNa,Cd�MHg�A�b�ܤj���@�ӷūd�U�ҩʽ�G
1�G
�b�C�������p�U�A���窺���G�P�z�Q����۪��A(�w�qcV�McP�����ռ��e�q)�z�Q���馳�U�ҩʽ�G(���ҥ���110��)
1�GcV is a function
of �c only 2�GcP
is a function of �c only 3�GcP��cV
= const. = R 4�G�^=cP/cV
= a function of �c only and >1 �C���ɪ����l����G�pHe,Ne�MAr�Τj�h�ƪ��ݻ]��pNa,Cd�MHg�A�b�ܤj���@�ӷūd�U�ҩʽ�G
1�G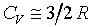 2�G
2�G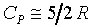 3�G
3�G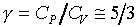 �C��������l�� ����lH2,D2,O2,N2,NO,CO��
1�G
�C��������l�� ����lH2,D2,O2,N2,NO,CO��
1�G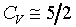 �A�b�`�ŮɬO�`�ơA�H�ūW�[���ܤj�C
2�G �A�b�`�ŮɬO�`�ơA�H�ūW�[���ܤj�C
2�G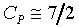 �A�b�`�ŮɬO�`�ơA�H�ūW�[���ܤj�C
3�G �A�b�`�ŮɬO�`�ơA�H�ūW�[���ܤj�C
3�G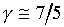 �A�b�`�ŮɬO�`�ơA�H�ūW�[���ܤp�C���h��l������l�A�άO���ʸ��j��������l�A�pCO2,
NH3, CH4, Cl2, Br2 ���A��Cv�A
Cp�Mg�H�ūפ��ܤƦӦ��ҧ��ܡA�B���ܤ��H����ӦU�����P�C��5-5�OH2���H�ū��ܤƪ����q�A�b�C�Ů� �A�b�`�ŮɬO�`�ơA�H�ūW�[���ܤp�C���h��l������l�A�άO���ʸ��j��������l�A�pCO2,
NH3, CH4, Cl2, Br2 ���A��Cv�A
Cp�Mg�H�ūפ��ܤƦӦ��ҧ��ܡA�B���ܤ��H����ӦU�����P�C��5-5�OH2���H�ū��ܤƪ����q�A�b�C�Ů�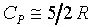 �A�`�Ů� �A�`�Ů�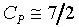 �A�Ӱ��Ůɬ�9/2�C������H�H�H�]���C�Ůɲ��ʮ�������A�ӶȦ��T�ӦۥѫסC�`�ŮɬO�P�ڭ̩ҹw���ۦP�A�h�F�����ʦۥѫסC���Ůɮ��ʪ���������{�C
�o���ܤơA�O�i�H�ί�q������z�������C(the
principle of the equipartition of energy)��q������z�O���C�@�ۥѫר��m(1/2)nRq������C��l������l���l�i�H���g�� �A�Ӱ��Ůɬ�9/2�C������H�H�H�]���C�Ůɲ��ʮ�������A�ӶȦ��T�ӦۥѫסC�`�ŮɬO�P�ڭ̩ҹw���ۦP�A�h�F�����ʦۥѫסC���Ůɮ��ʪ���������{�C
�o���ܤơA�O�i�H�ί�q������z�������C(the
principle of the equipartition of energy)��q������z�O���C�@�ۥѫר��m(1/2)nRq������C��l������l���l�i�H���g��
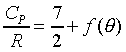
�䤤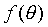 �O����άO �O����άO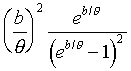 ���զ��C ���զ��C
5-5 ���R�������L�{
�]��
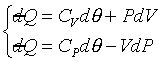 �A �A
�B�����L�{�� ,
�ҥH ,
�ҥH
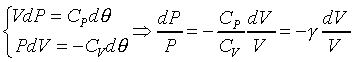
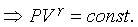
This equation holds at all equilibrium states
through which an ideal gas passes during a quasi-static adiabatic process. �@�t�C�������L�{�i�H���ܦbPV�۹ϤW�A��ײv��
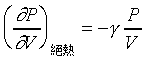
���R�����ŹL�{�]�i�H�Q�@�t�C�����u���ܡA��ײv��
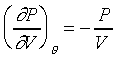 �Y �Y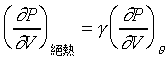 �A �A
�����L�{���ײv���j�C
5-6 Ruchhardt's Method �� g
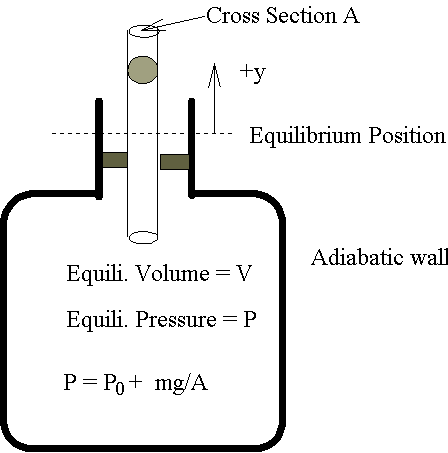
y �ܤp�A���p�y��qm�A�Q�U��y������A�|����²�ӹB�ʡC�]�g����t�A�b���Ҽ{�����O�����p�U(P0
���j����)
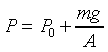
��n���ܤ�dV=yA�A�����O���ܤƬ�
dP=F/A�A�䤤F���X�O���j�p�C�]�����ʧֳt�A�ҥH�L�{�i�H���������A�BdV�BdP���ܤp�A�G�L�{�i�H�����źA�C�Q�ε����L�{������o

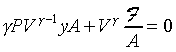
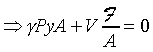
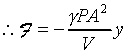 �A �A
�o�O�P��J�w�߬ۦ��A�G�P���O
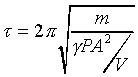 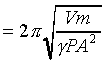
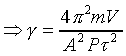 �A �A
�p���h�i�H�D�Xg�C�Q�γo�ؤ�k�q�����~�t�ӷ����@)
����D�z�Q���� �G) �������s�b
�T) The volume change is strictly adiabatic, but
it is not absolutely adiabatic. The modified Ruchhard's experiment to get more
accurate data can be found in the text book.
5-7 Speed of a Longitudinal wave
In this section we want to how g
paly the role in the longitudinal wave. ���@����(�Ψt��)���Y�@�����Q���Y��A�����Y�������N�|���t�v�Aw�A�ǻ��ܨ䥦�����A���t�v���j�p�P�զ����誺���観���C�U�Ϥ��A�p�G����Q�I�O
P+DP
�V�k�H���t�סAw0�A���ʮɡA�|�������Y(compression)�H���t��w�B�ʡC�����Y��iwt�Z���ɡA���벾��w0t���Z���C
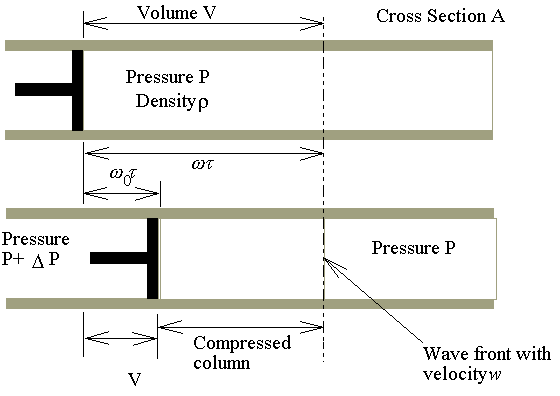
�ҥ������k�G��ӨS�����Y�ϡA�������Yt�ɫ�A�l�����Y�Ϫ����͡C�G���Y�Ϫ���q�W�[�v��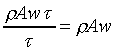 �A �A
�B������Y�Ϥ��誺�t��w0�A���Y�ϰʶq�H�ɶ����W�[�q(Dp/Dt)��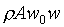 �C�t�@�جݪk�O���Y�Ͻ�q�W�[���t�v�� �C�t�@�جݪk�O���Y�Ͻ�q�W�[���t�v��
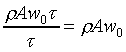
(�Ҽ{����Q���Yw0t)�A���Y�ϰʶq�H�ɶ����W�[�q(Dp/Dt)��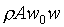 �A��ڤ��y�ĤG�B�ʩw�ߡA�i�H���p�U�����l �A��ڤ��y�ĤG�B�ʩw�ߡA�i�H���p�U�����l
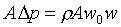
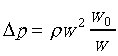
�䤤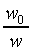 �P���Y����n���ܪ���Ҧ����A�ҥH �P���Y����n���ܪ���Ҧ����A�ҥH
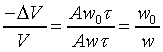
�h���Y�Ϥ����O������DP��
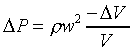
�άO���Y�Ϫ��t�O
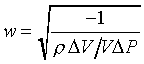
���������Ѥ��y�ɥX�A�����t���@�q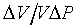 �A���y�{���O�������Y�Y��(Isothermal
Compressibility)�A����ڤW�O�������Y�Y�ơC�p�G�ڭ̦Ҽ{��Ӱ��Q���A�@�b���Y�Ϫ����ߡA�t�@�b�}���Ϥ��ߡA��̤������Z���� �A���y�{���O�������Y�Y��(Isothermal
Compressibility)�A����ڤW�O�������Y�Y�ơC�p�G�ڭ̦Ҽ{��Ӱ��Q���A�@�b���Y�Ϫ����ߡA�t�@�b�}���Ϥ��ߡA��̤������Z����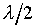 �A�ūt��Dq�C���Q���Y�i��i�ɡA�ҶǾɪ����q�� �A�ūt��Dq�C���Q���Y�i��i�ɡA�ҶǾɪ����q��
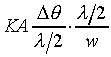 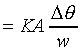
K��������餧���ǾɫY�ơC�b�ŮtDq��������q��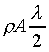 �A�Ӳ��ͦ��Ůt�һݤ����� �A�Ӳ��ͦ��Ůt�һݤ�����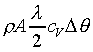 �C�p�G���Y�i���ǻ��O�������A�����O�ǻ������Ӥ֦ӵL�k�N�䶡��q�� �C�p�G���Y�i���ǻ��O�������A�����O�ǻ������Ӥ֦ӵL�k�N�䶡��q��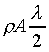 �����貣��Dq���Ůt�A�Y �����貣��Dq���Ůt�A�Y
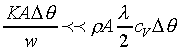
�]�N�O������������O
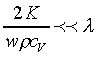
In general, the typical wavelength is from a few
centimeters to several hundred centimeters. For gas at 0�J,
we have 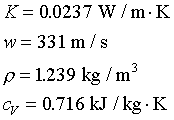
therefore
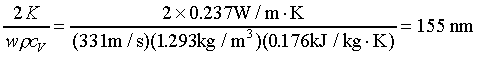
which is much smaller than the wavelength. In
the case of metal, K would be larger, but this will be compensated by the
much larger values of w and q,
hence it will be still smaller than 155 nm. Therefore the adiabatic condition is
fulfilled. The volume changes which take place under the influence of a
longitudinal wave at ordinary frequencies are adiabatic, not isothermal.
Let
-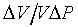 = kS,
= kS,
as the adiabatic compressibility. So
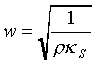
For ideal gas
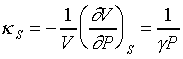
and
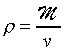
where M
is the molar mass and v is the molar volume. Hence
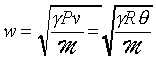 or
or
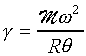
For example, the speed of sound in are at 0�J
is about 331 m/s, M
for air is 28.96 kg/kmol, therefore g
is 1.40. The speed of sound wave in a gas can be measured roughly by means of
Kundt's tube.
5-8 Acoustical Thermometry(�i�H�ΨӶq���z�Q�����)
In previous section, we discuss the longitudinal
wave in a tube. For more accurate measurement, the instrument equiped with an
acoustic interferometer, one end of the tube is a source of waves such as a
piezoelectric crystal and at the other a receiver. The distance of source and
receiver is kept constant, the frequency of wave can be varied, the various
resonances are reached. We can also use this equipment to determine the ideal
gas temperature �c by plotting the square of
the speed of sound as a function of pressure. Then
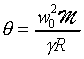
where 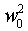 is the extrapolation of the square of the speed of sound to zero pressure, which
assures ideal conditions.(����5-11)
is the extrapolation of the square of the speed of sound to zero pressure, which
assures ideal conditions.(����5-11)
5-9 The Microscopic point of view
�j����O�ǬO�إߦb�t�Υ��[���欰�W�A�ΥH�y�z�t�Ϊ����z�q�]�O���[�������ȡC�Ĥ@�w�ߥH��q�u�ڪ��k�h�A�N���B�\�M����sô�b�@�_�C���Ĥ@�w�����Ψ�P�@�������t��(�p�R�y��)�ұo�����Y��������������@�t�Χ����ߡA�]�N�O�����Ҽ{(�λ��L�k�Ҽ{)�U�P���t�Τ��L�[�ʽ誺�t���C�Ҧp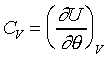 ��Ҧ��R�y��t�Τ����T��B�G��M���駡���ߡC�p�G���DU�MV�B�c�����Y�A�ڭ̥i�H�p��CV�C�b����n�L�{���A�p�G��CV�M�c�����Y�A���q�i�H�ѤU����X: ��Ҧ��R�y��t�Τ����T��B�G��M���駡���ߡC�p�G���DU�MV�B�c�����Y�A�ڭ̥i�H�p��CV�C�b����n�L�{���A�p�G��CV�M�c�����Y�A���q�i�H�ѤU����X:
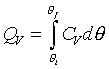 ���O����CV�MU�����Y���Բ����s�A�j����O�ǫo�L�k�J�Ӫ����ѡA��U
�i�H�ηL�[����k�p��ӱo�C�j����O�Ǫ��t�~�@�ӷ����O�L�k��X�βz�ɥX���A��{���C�t�Ϊ����A��{���A�h�b�ѹ����k�M�w�C�Ҽ{��t�ηL�[�ʽ誺�z�צ��G�G�@�O����ʤO��(Kinetic
Theory)�A�t�@�O�έp�O��(Statistical
Mechanics)�C����̥H�Ҽ{���l�B�ʬ��۲��A�p�I���A�@�ΤO�A��q���C����ʤO��(Kinetic
Theory)�i�H�B�z�U�z�D���Ū����A:(�Ѩ�O�G�A�t��)
�@) Effusion�G���l�Ѯe���p�պ��z�X�Ӫ��L�{�C
�G) Laminar Flow�GMolecules
moving through a pipe under the action of a pressure difference. �T)
Viscosity�GMolecules with momentum moving
across a plan and mixing with molecules of lesser momentum. �|)
Heat Conduction�GMolecules with kinetic
energy moving across a plan and mixing with molecules of lesser energy. ��)
Diffusion�GMolecules of one sort moving
across a plane and mixing with molecules of another sort. ��)
Chemical Kinetics�G��ةΦh�ؤƾǤ��l�������t�v���ƾǵ��X
�C) Brownian Motion�G
�έp�O�ǥѤ��l��q���[�I�X�o�A��Ũt�Υi�H�������ܦn�A�����D���Ũt����t�����۷��j���Ŷ��ݭn�h�F�ѡC
5-10 Kinetic Theory--Equation of state of an ideal
gas ��²�檺����ʤO�רD�z�Q���骺���A��{���C����]��
�@)����@�t�Ωҥ]�t���ɤl�ơAN�A���D�`�j�A�B�~�[���ۦP�L�k�ϧO�C�Ҧp�z�Q����b�@�j�����U0�J����n��2.24��104cm3�A����6.0225��1023�Ӳɤl�C��n��
1 cm3�A��3��1019�Ӳɤl�C��n��
1 mm3�A��3��1016�Ӳɤl�C��n��
1 mm3�A��3��107�Ӳɤl�C�G)
�z�Q������l�Ѥp�ӵw���y�Ҳզ��A�B���H���B�ʡC���l����n�i�H�Q�����A�λ����l�������Z�������l���j�p�j�\�h�C�T)
�z�Q������l���S�����@�ΤO�A�p�l�ޤO�B�ƥ��O���C
�|)
�z�Q������l�����I�������u�ʸI���A�P�����I���笰�u�ʸI���C��)
�z�Q������l�B��L�~�O�@�Ϊ����p�U�ɡA�����O���ê��C
��) �z�Q������l�B�ʳt�פ�V�S���S�w�����V�C(�]�N�O�U��V�B�ʪ��ɤl�ƬO�@�˦h�C�C)
�z�Q������l�B�ʳt�O�@���G�A�C�@���l���B�ʳt�׳����P�C
�t�פ�V�S���S�w�����V�A�Ҽ{�@���N���t�צV�qw�A�p��5-12�ҥܡA�ѭ��I�쭱�ndA'�A�����n�ҹ��������騤�� ���O����CV�MU�����Y���Բ����s�A�j����O�ǫo�L�k�J�Ӫ����ѡA��U
�i�H�ηL�[����k�p��ӱo�C�j����O�Ǫ��t�~�@�ӷ����O�L�k��X�βz�ɥX���A��{���C�t�Ϊ����A��{���A�h�b�ѹ����k�M�w�C�Ҽ{��t�ηL�[�ʽ誺�z�צ��G�G�@�O����ʤO��(Kinetic
Theory)�A�t�@�O�έp�O��(Statistical
Mechanics)�C����̥H�Ҽ{���l�B�ʬ��۲��A�p�I���A�@�ΤO�A��q���C����ʤO��(Kinetic
Theory)�i�H�B�z�U�z�D���Ū����A:(�Ѩ�O�G�A�t��)
�@) Effusion�G���l�Ѯe���p�պ��z�X�Ӫ��L�{�C
�G) Laminar Flow�GMolecules
moving through a pipe under the action of a pressure difference. �T)
Viscosity�GMolecules with momentum moving
across a plan and mixing with molecules of lesser momentum. �|)
Heat Conduction�GMolecules with kinetic
energy moving across a plan and mixing with molecules of lesser energy. ��)
Diffusion�GMolecules of one sort moving
across a plane and mixing with molecules of another sort. ��)
Chemical Kinetics�G��ةΦh�ؤƾǤ��l�������t�v���ƾǵ��X
�C) Brownian Motion�G
�έp�O�ǥѤ��l��q���[�I�X�o�A��Ũt�Υi�H�������ܦn�A�����D���Ũt����t�����۷��j���Ŷ��ݭn�h�F�ѡC
5-10 Kinetic Theory--Equation of state of an ideal
gas ��²�檺����ʤO�רD�z�Q���骺���A��{���C����]��
�@)����@�t�Ωҥ]�t���ɤl�ơAN�A���D�`�j�A�B�~�[���ۦP�L�k�ϧO�C�Ҧp�z�Q����b�@�j�����U0�J����n��2.24��104cm3�A����6.0225��1023�Ӳɤl�C��n��
1 cm3�A��3��1019�Ӳɤl�C��n��
1 mm3�A��3��1016�Ӳɤl�C��n��
1 mm3�A��3��107�Ӳɤl�C�G)
�z�Q������l�Ѥp�ӵw���y�Ҳզ��A�B���H���B�ʡC���l����n�i�H�Q�����A�λ����l�������Z�������l���j�p�j�\�h�C�T)
�z�Q������l���S�����@�ΤO�A�p�l�ޤO�B�ƥ��O���C
�|)
�z�Q������l�����I�������u�ʸI���A�P�����I���笰�u�ʸI���C��)
�z�Q������l�B��L�~�O�@�Ϊ����p�U�ɡA�����O���ê��C
��) �z�Q������l�B�ʳt�פ�V�S���S�w�����V�C(�]�N�O�U��V�B�ʪ��ɤl�ƬO�@�˦h�C�C)
�z�Q������l�B�ʳt�O�@���G�A�C�@���l���B�ʳt�׳����P�C
�t�פ�V�S���S�w�����V�A�Ҽ{�@���N���t�צV�qw�A�p��5-12�ҥܡA�ѭ��I�쭱�ndA'�A�����n�ҹ��������騤��
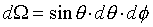 (�̤j���騤���q��4p)�] (�̤j���騤���q��4p)�]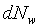 �O�t�פ���w��w
+ dw�������`�ɤl�ơA�ӳt�פ���w��w
+ dw�����B��V�O�µۥ��騤 �O�t�פ���w��w
+ dw�������`�ɤl�ơA�ӳt�פ���w��w
+ dw�����B��V�O�µۥ��騤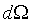 ���ɤl�ơA ���ɤl�ơA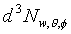 �A�� �A��
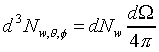 �W���]�����z�Q������l�B�ʳt�פ�V�S���S�w�����V�C�Ҽ{�@��W������ndV�A�p��5-13�ҥܡA
�W���]�����z�Q������l�B�ʳt�פ�V�S���S�w�����V�C�Ҽ{�@��W������ndV�A�p��5-13�ҥܡA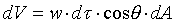 �C�Y�]V�O�`��n�A�h�u���b��W�������l���Ҧ��`���l�ƪ���Ҭ� �C�Y�]V�O�`��n�A�h�u���b��W�������l���Ҧ��`���l�ƪ���Ҭ�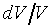 �A�h
Number of w, �c,
f molecules
striking dA in time dt = �A�h
Number of w, �c,
f molecules
striking dA in time dt =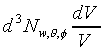 �W�����ܲz�Q������l���G�O���ê��C�t�@���]�O�Ҧ����I�����O�u�ʸI���A�h�H�c�J�g�ӸgdA�ϼu�����l��ʶq�����ܬ�
�W�����ܲz�Q������l���G�O���ê��C�t�@���]�O�Ҧ����I�����O�u�ʸI���A�h�H�c�J�g�ӸgdA�ϼu�����l��ʶq�����ܬ�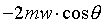 �A�]���u���������q���ܤơC�G�H�c�J�g�ӸgdA�ϼu���Ҧ��z�Q������l�ҳy���`�ʶq�����ܬ� �A�]���u���������q���ܤơC�G�H�c�J�g�ӸgdA�ϼu���Ҧ��z�Q������l�ҳy���`�ʶq�����ܬ�
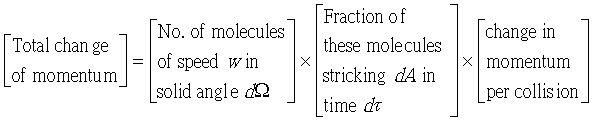 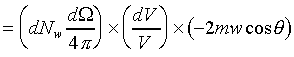
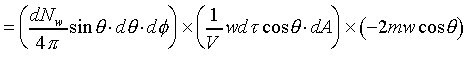
�g�ѸI���Ӳ��ͤ���쭱�n���ɶ����ʶq�����ܬO�������O�C�]���O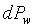 ����I���ѦU�Ӥ�V�� ����I���ѦU�Ӥ�V��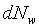 �Ӯ�����l�����O�C�h���ܰʶq���ܪ����t���A�i�H�o��U�Ӥ�V������ �Ӯ�����l�����O�C�h���ܰʶq���ܪ����t���A�i�H�o��U�Ӥ�V������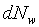 ������l�I�������O ������l�I�������O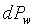 �A�Y �A�Y
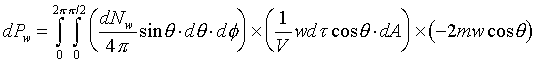
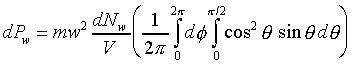
�]��
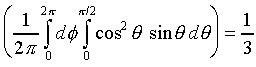 �A �A
�ҥH
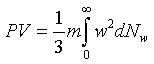
�Ӥ��l�t�ץ��誺�����ȬO
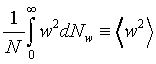 �A �A
���t�X
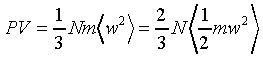 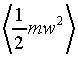
����C�Ӥ��l�������ʯ�A�P��������o
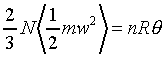
�ҥH�C�@�Ӥ��l�������ʯ��(�P��q�����w�z���G�ۦP)
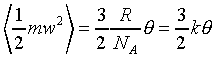
k�i���ұ`�ơA��ȵ���1.3805��10-23
J/K�C ���G�t�~�@�ظѪk�O�N�t�ΦҼ{��������A�h The
momentum change for the collision per molecule is
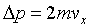
and the average per collision is
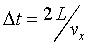 �C �C
The force due to one collision is
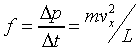 �A �A
thus the pressure on the suface is
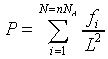 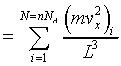 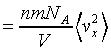 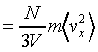
This is the same result we have discussed above.
�@ | 