|
我們設計了一個一維高斯波包(Gaussian Wave Packet)遇到不同位能障礙時其機率密度變化的情形。
機率密度:
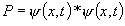
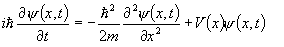 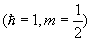
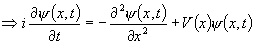
然後,利用Crank-Nicholson的差分法:(n->時間切割,j->空間切割)
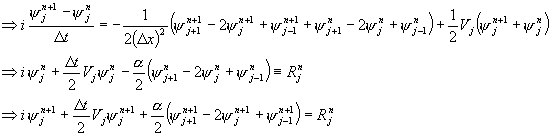
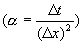
可以將上式寫成矩陣方程如下:
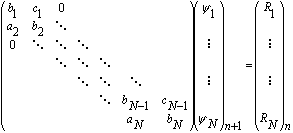
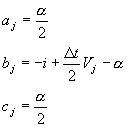
接著,以數值方法解三對角化矩陣(tridiagonal
matrix),求得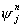 ,j=1,2,....,N。 ,j=1,2,....,N。
一直利用疊代法的方式從 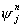 求出下一刻
求出下一刻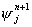 ,依此類推就能求出每個時刻的波函數。 ,依此類推就能求出每個時刻的波函數。
參考資料:
Numerical
Recipes: The Art of Scientific Computing
(FORTRAN version)
William
H. Press
Brian P. Flannery
Saul
A. Teukolsky
William T.Vetterling
(Crank-Nicholson的數值方法---page
640)
(解
Tridiagonal
System
of Equation---page 40)
|