Chapter 6 Engines, Refrigerators and the second law of Thermodynamics

6-1 Conversion of work into heat and vice versa

Conversion work into heat: (System do the work which transfer and become heat to the surroundings)

一) The state of system does not change.

二) 100 % efficiency.

三) This transformation can be continued indefinitely.

Examples :

• Running water go through a constant current resistor, water take the heat and does not change the state of resistor.

• Rub two stones under a large tank, and can have water take out the heat and does not change the state of stones.

Transformation of heat into work: (Heat input by the surroundings and system do work)

一) System state changed.

二) It is not 100 % efficiency.

三) It can not be operated indefinitely.

四) It must be performed in a CYCLE.

Example: For isothermal process in an ideal gas system; the internal energy of system will not change, and

-W = Q =,

heat has been converted completely into work, but the involved the change of state of the gas. The volume increase and the pressure decrease until the normal pressure is reached, at which the process stops, so it can not be used indefinitely. Therefore the system has to be brought back to initial state ( i.e. a cycle), which involve a flow to or from the system and the performance of work by or on the system to complete a cycle.

Thermal efficiency h: It is the ratio of work output to heat input.

heat rejected by the system is

Engines : Transformation of heat into work.

一) The external-combustion engine: such as the Stirling engine and the steam engine.

二) The internal-combustion engine: such as gasoline engine and the diesel engine.

Common: Both type of engines have a cylindrical container which contains a gas or mixed of gas, during combustion the temperature and pressure of the gas are very high.

Difference: The combustion done by outside agent is called external-combustion engines and the combustion done by the gas itself is called external-combustion engines.

6-2 The Stirling Engine

History : In 1816, before the science of thermodynamics had been begun, a minister of the Church of Scotland named Robert Stirling designed a hot-air engine which can convert some of the heat from burning fuel into work.

Advantage: Low exhaust emission and high efficiencies.

Disadvantage : High manufacturing costs. Idealized Stirling Engine are shown in the following, which is based on some assumptions, and they are :

1) the gas is ideal,

2) no leakage of gas takes place,

3) no heat is lost or gained through cylinder walls,

4) no heat is conducted through the regenerator,

5) there is no friction.

The Stirling Cycle diagram is

1→2 It is an isothermal process, the piston in contact with cold reservoir is compressed isothermally, hence heat |QC| has been rejected, and (isothermal compression → dU = 0, W is positive and QC is negative) the heat rejected is

2 → 3 It is an isochoric process, the left piston moves down while the right piston moves up. The volume of system is kept constant, thus no work has been done by the system, but heat QR has been input to the system by the regenerator which causes temperature to raise to qH.

3 → 4 It is an isothermal expansion process, the left piston in contact with hot reservoir expanded isothermally at temperature qH. Therefore

4 → 1 It is an isochoric process which is a reversed process of 2 → 3, but from qH to qC. The efficiencies of Stirling engine is

and work done by the system to the surroundings is|W| = |QH| - |QC|.

6-3 Steam Engine

The process of steam engine can be described as following

To analyze the process of a steam engine is very difficult, because

(1) acceleration and turbulence caused by the pressure difference required to cause the flow of the stem from on part of the apparatus to another,

(2) friction,

(3) conduction of heat through the walls during expansion of the steam,

(4) heat transfers due to a finite temperature difference between the furnace and boiler, these properties are not easy to control and define.

Rankine Cycle:

1) an approximation for describing the process of steam engine.

2) Define the upper limit of the efficiency of steam engine.

1 → 2 Adiabatic compression of water to the pressure of the boiler ( only a very small change of temperature takes place during this process).

2 → 3 Isobaric heating of water to the boiling point.

3 → 4 Isobaric, isothermal vaporization of water into saturated steam.

4 → 5 Isobaric superheating of steam into superheated steam at temperature qH.

5 → 6 Adiabatic expansion of steam into wet steam.

6 → 1 Isobaric, isothermal condensation of steam into saturated water at the temperature qC, and rejected heat |QC|.

During the processes 2 → 5, heat |QH| enters the system from a hot reservoir whereas during the condensation process 6 → 1, heat |QC| is rejected by the system to a reservoir qC. The output work per cycle is W = |QH| - |QC|. Heat is always rejected during condensation, thus |QC| can not be made equal to zero.

6-4 Internal-Combustion Engine

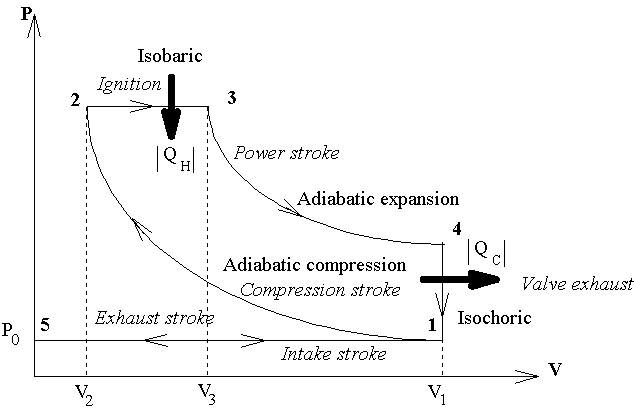
The cycle involved in the internal combustion engines have

1) six processes, and

2) four strokes

which require the motion of piston. They are described as follow:

1) Intake stroke.

2) Compression stroke.

3) Ignition.

4) Power stroke.

5) Valve exhaust.

6) Exhaust stroke.

Otto Cycle : Idealized gasoline engine performed as Otto cycle, describe as follow

The above diagram based on some assumptions and they are:

1) The working substance is at all times air, actually ideal gas with constant heat capacities.

2) All processes are quasi-static.

3) No friction.

5 → 1 Isobaric intake at 1 atm, thus

.

1 → 2 Adiabatic compression, temperature raised from q1 to q2, then

2 → 3 Isochoric process. To increase the temperature from q2 to q3, and pressure at constant volume V2, heat |QH| is absorbed, assume constant CV,

3 → 4 Adiabatic expansion, the temperature drop from q3 to q4, thus

4 → 1 Isochoric process, heat |QC| is rejected, temperature is dropped from q4 to q1, and pressure is dropped to 1 atm. Assume constant CV, we have

1 → 5 Isobaric exhaust at 1 atm with temperature at q1. This is a reversed process of 5→1.

The efficiency of the ideal gasoline engine is

and

, thus

,

so

where r is called compression ratio, r can not be greater than 10, because it will combustion before advent of the spark (this is called preignition), thus the maximum h is (take r=9, =1.5)

The actual gasoline engine has efficiency much lower than 67%.

Air-Standard Diesel Cycle : For Diesel engine, intake stroke only take air into cylinder, then compress the air adiabatically to the temperature high enough to ignite the oil that is sprayed into the cylinder. The ignition process is isobaric.

For constant specific heat at constant pressure and constant volume, we have

and

,

also

the adiabatic processes give other two relations

and

and

where

,

so

Diesel engine does not have the problem of preignition because the oil is sprayed when ignition. For rC = 15, rE = 5, g = 1.5, we have h = 64 %.

Two stroke cycle Ddiesel engine : the intake stroke and exhaust stroke is completed at the end of power stroke by using a air blower to blow the combustion products, in the mean time the fresh is also blown into the cylinder.

6-5 Kelvin-Planck statement of the second law of thermodynamic

The characteristics of heat engine cycles are :

1) There is some process of series of processes during which there is an absorption of heat from a hot reservoir.

2) There is some process or series of processes during which there is a rejection of heat to cold reservoir.

3) There is some process or series of processes during which the work is delivered to the surroundings.

The conclusion is " No engine has ever been developed that converts the heat extracted from one reservoir into work without rejecting some heat to a reservoir at a lower temperature."

The second law of thermodynamics :

(A) The original statement of Kelvin: " It is impossible by means of inanimate material agency to derive mechanical effect from any portion of matter by cooling it below the temperature of the coldest of the surrounding objects. "

(B) Plank's statement " It is impossible to construct an engine which, working in a complete cycle, will produce no effect other than the raising of a weight and the cooling of a heat reservoir. "

(C) Kelvin-Plank statement : " No process is possible whose sole result is the absorption of heat from a reservoir and the conversion of this heat into work. "

The first law is based on the energy conservation law, and it denies the possibility of creating or destroying energy. But it did not say that internal energy can not be converted solely into heat or into work. Neither does it not restrict that heat convert solely into work, which violate the second law. The second law denies the possibility of utilizing energy in a particular way, for example convert heat completely into work.

6-6 Refrigerator

Heat engine : Some heat is absorbed by the system from a hot reservoir, hence system can do the work to the surroundings, then a smaller amount of heat is rejected to the cold reservoir. A net amount of work is done to the surroundings during one cycle.

Refrigerator : (reverse the cycle of heat engine) Absorption some heat from cold reservoir and reject it to the hot reservoir, also a net among of work is done to the system from its surroundings. This system is called refrigerant.

The Stirling cycle is capable of being reversed, when reversed, it gives rise to one of the most useful types of refrigerator.

The schematic diagram for electric home refrigerators is shown below, a constant mass of refrigerant is stored in the liquid storage which have the same temperature and pressure as it in the condensor. The refrigerant go through the throttling valve, through the evaporator, into the compressor and finially back to the condensor.

The refrigerant, while it being compressed in the condenser then stored in the liquid storage, is at a high pressure and at as low a temperature as can be obtained with air or water cooling, and it is a saturated liquid. Adiabatically undergo a throttling process, or a Joule-Thomson or Joule-Kelvin expansion, always produces cooling and partial vaporization. In the evaporator the fluid is completely vaporized, the heat to vaporize these liquid is supplied by the materials to be cooled. The vapor is then compressed adiabatically, therefore the temperature is increased. In the condenser the vapor is completely liquefied. The PV diagram of refrigerator cycle is

1 → 2 Throttling process involving a drop of pressure and temperature can not be represented by thermodynamic coordinates.

2 → 3 Isothermal, isobaric vaporization, and heat QC is absorbed by the refrigerant.

3 → 4 Adiabatic compression of the vapor to a temperature high than that of the condenser qH.

4 → 1 Isothermal and isobaric cooling and condensation.

(Definition :

Output of refrigerator: is the heat extracted from the cold reservoir.

Input of refrigerator: is the work done to the refrigerant by the compressor)

Coefficient of performance (or cooling energy ratio ) w

w for commerical build refrigerator is about 2 to 7. For the case of w = 5, that is

which gives

,

this means the heat liberated at the higher temperature is equal to six times the work done. In this case, if the work is supplied by an electric motor, for every joule of electrical energy supplied, 6 J of heat will liberated, it is a very good ideal to build a heater to warm the house by refrigerating the outdoors. ( In general, use resister as heater, which 1 J of electrical energy can only give 1 Joule of heat.) This heater idea is first point out by Lord Kelvin, but the first heater to heat a house is built by Haldane.

The Clausius Statement of the Second Law : " No processes is possible whose sole result is the transfer of heat from a cooler to a hotter body. " That is, the process of the heat trasnfered from cold reservoir to hot reservoir has to be accomplished with supplied work.

6-7 Equivalence of Kelvin-Plank and Clausius Statement

Notations:

K = truth of the Kelvin-Plank statement

-K = falsity of the Kelvin-Plank statement

C = truth of the Clausius statement

-C = falsity of the Clasusius statement

= imply

= equivalence

When K C and C K, then K C. Also, when -K -C and -C -K, then K C. We prove the equivalence of Kelvin-Plank statement and Clausius statement by proving that " when -K -C and -C -K, then K C ".

1) First we prove -C -K,

2) Then we prove -K -C,